Table of Contents

Recap
Incorporating Slippage
Slippage Costs
Cutting It Short

Recap

In our last article we had a look at how to rebalance positions based on an error threshold instead of doing it daily to reduce transactions and trading costs. We're now only adjusting our positions when our current risk deviates more than 10% from the ideal risk.

We're almost finished with our backtest. There are still some kinks we need to iron out before we can really use it for strategy development though. So let's get right to it!

Incorporating Slippage

First, let's quickly reiterate what slippage is:

Slippage is the difference between the price you think you'll be trading at and the price you're actually trading at. Just because you tried to enter a trade immediately after the close, doesn't mean you'll always get that price. Prices tend to be noisy, especially around higher timeframe closes. Lot's of other people use the same timeframe as we are so we're not going to be the first in line to trade right away. Depending on the instruments volatility, liquidity and our size and the exchanges matching mechanism, we're going to get served for different prices than intended, especially when using market orders.

For our model, slippage is not all that important. Since we probably only want to trade the most liquid instruments on the daily timeframe with very little size (total of $10,000 bankroll), we don't care all that much about things like market impact. It is enough for us to simply apply a standard pnl reduction to each trade to account for slippage.

So what amount of slippage should we deduct? Again, slippage depends on the size we're trading, current orderbook liquidity, etc. We're going to continue to assume that the current orderbook supports our trades without blasting through it. We mainly want to simulate not getting filled right at the top but maybe one level below that because we weren't first in line.

Assuming slippage of 0.01% to 0.05% or 1 to 5 basis points (bps) respectively is going to be enough. If you want to take it up a notch to purposely simulate higher volatility environments or stress test your model you can let it spike to 0.1% or even 0.25%.

To apply the slippage correctly, which is basically price moving against us, we need to know the direction of the position we're taking and then adjust the close price accordingly:

COPY[...]
slippage_percent = 0.1
slippage_percent_dec = slippage_percent / 100

for index, row in df.iterrows():
    [...]
    # simulate trading
    if df.index.get_loc(index) > 0:
        [...]

        # we're trading
        if contract_deviation > rebalance_err_threshold:
            if ideal_pos_contracts > 0:
                position_direction = 1
            else:
                position_direction = -1
            df.at[index, 'position_direction'] = position_direction

            slippage_amount_per_contract = row['close'] * slippage_percent_dec
            close_slipped = row['close'] + slippage_amount_per_contract if position_direction >= 0 else row['close'] - slippage_amount_per_contract
            df.at[index, 'close_slipped'] = close_slipped

            [...]

The above code re-calculates the price we would've executed at based on our configured slippage of 0.1% (10 bps) if we had traded 1 contract. Next we need to adjust this figure to the amount of contracts actually traded:

COPY# we're trading
if contract_deviation > rebalance_err_threshold:
    if ideal_pos_contracts > 0:
        position_direction = 1
    else:
        position_direction = -1
    df.at[index, 'position_direction'] = position_direction

    slippage_amount_per_contract = row['close'] * slippage_percent_dec
    close_slipped = row['close'] + slippage_amount_per_contract if position_direction >= 0 else row['close'] - slippage_amount_per_contract
    df.at[index, 'close_slipped'] = close_slipped

    slippage_paid = abs(contract_diff) * slippage_amount_per_contract * contract_unit
    df.at[index, 'slippage_paid'] = slippage_paid

    rebalanced_pos_contracts = ideal_pos_contracts
    notional_traded = contract_diff * notional_per_contract
else:
    slippage_paid = 0
    rebalanced_pos_contracts = current_pos_contracts
    notional_traded = 0

Deducting the costs from our performance now becomes really easy, we just substract it from our pnl:

COPY# Calculating Performance
instr_raw_returns = df['instr_price_returns']
strat_raw_usd_returns = df['rebalanced_pos_contracts'].shift(1) * instr_raw_returns
df['strat_raw_usd_returns'] = strat_raw_usd_returns.fillna(0)

# Deduct fees
strat_usd_returns = df['strat_raw_usd_returns'] - df['fees_paid']
df['strat_usd_returns_after_fees'] = strat_usd_returns
df['strat_usd_returns_postcost'] = df['strat_usd_returns_after_fees']


# Deduct slippage
strat_usd_returns = df['strat_usd_returns_after_fees'] - df['slippage_paid']
df['strat_usd_returns_after_slippage'] = strat_usd_returns
df['strat_usd_returns_postcost'] = df['strat_usd_returns_after_slippage']

[...]
# Deduct funding
# Calculate SR

Slippage Costs

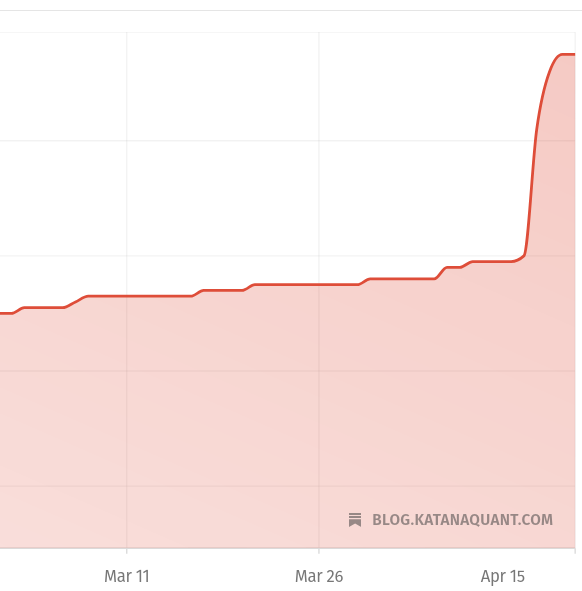
Let's run our backtest again.

COPY# Strategy Total Return 948.9002953840393
# Strategy Avg. Annual Return 65.07865610957803
# Strategy Daily Volatility 1.8181518825213718
# Strategy Sharpe Ratio 1.8735357472190997

# Fees paid 1038.6238698915147
# Slippage paid 1888.4070361663905
# Funding paid 3130.3644113437113

# Strategy Ann. Turnover 37.672650094739545

# Pre-Cost SR 1.9914208916281093
# Post-Cost SR 1.8735357472190994
# Risk-Adjusted Costs 0.11788514440900988

# [...]

We paid a total of $1,888 in slippage. As you can see this is far more than the $1,038 fees paid. This is due to the fact that we set the slippage fairly high to 0.1%. I like to stay on the more conservative side and keep it this high for now.

Our risk adjusted costs increased from ~ 0.0731 SR units to ~0.1179; about ~61.3%. Definitely nothing to sneeze at!

Since our model is using market orders, we also have to pay the bid-ask spread. For this model, where we want to trade only the most liquid instruments, we're going to assume that the bid-ask spread is already accounted for via our slippage calculations.

Cutting It Short

This is it for this week. I'm still quite tangled up in some personal and work matters so this article too is a rather short one. As soon as these get sorted out, the output will increase again. Promise!

The full code can be found here